2015年重庆双桥中考数学真题及答案A卷(WORD文档)
发布于 2021-09-03 14:13 ,所属分类:重庆中考真题试卷及答案大全
2015年重庆双桥中考数学真题及答案A卷
(全卷共五个大题,满分150分,考试时间120分钟)
参考公式:抛物线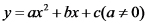 的顶点坐标为
的顶点坐标为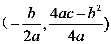 ,对称轴为
,对称轴为 .
.
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,期中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。
1.在—4,0,—1,3这四个数中,最大的数是( )
A. —4 B. 0 C. —1 D. 3
2. 下列图形是轴对称图形的是( )




A. B. C. D
3.化简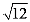 的结果是( )
的结果是( )
A. 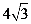 B.
B. 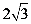 C.
C. 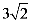 D.
D. 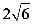
4.计算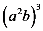 的结果是( )
的结果是( )
A. 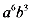 B.
B. 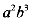 C
C .
. 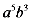 D.
D. 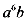
5.下列调查中,最适合用普查方式的是( )
A. 调查一批电视机的使用寿命情况
B. 调查某中学九年级一班学生视力情况
C. 调查重庆市初中学生锻炼所用的时间情况
D. 调查重庆市初中学生利用网络媒体自主学习的情况
6.如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H。若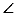 1=135°,则
1=135°,则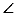 2的度数为( )
2的度数为( )
A. 65° B. 55° C. 45° D. 35°
7.在某校九年级二班组织的跳绳比赛中,第一小组五位同学跳绳的个数分别为198,230,220,216,209,则这五个数据的中位数为( )
A.220 B. 218 C. 216 D. 209
8.一元二次方程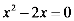 的根是( )
的根是( )
A.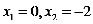 B.
B. 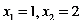
C. 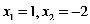 D.
D. 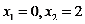
9. 如图,AB是 的直径,点C在
的直径,点C在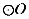 上,AE是
上,AE是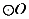 的切线,A为切点,连接BC并延长交AE于点D, 若
的切线,A为切点,连接BC并延长交AE于点D, 若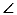 AOC=80°,则
AOC=80°,则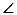 ADB的度数为( )
ADB的度数为( )
A. 40° B. 50° C. 60° D. 20°
10. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,
中途休息了一段时间,设他从山脚出发后所用的时间为t(分钟),
所走的路程为s(米),s与t之间的函数关系如图所示,
下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬上的速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平 均速度大于休息后爬山的平均速度
均速度大于休息后爬山的平均速度
11. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,其中第②个图形中一共有9个小圆圈,其中第③个图形中一共有12个小圆圈,...,按此规律排列,则第⑦个图形中小圆圈的个数为( )

①  ② ③
② ③
A. 21 B. 24 C. 27 D. 30
12.如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与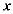 轴平行,A,B两点的纵坐标分别为3,1,反比例函数
轴平行,A,B两点的纵坐标分别为3,1,反比例函数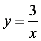 的图像经过A,B两点,则菱形对ABCD的面积为( )
的图像经过A,B两点,则菱形对ABCD的面积为( )
A. 2 B. 4 C.  D.
D. 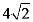
二、填空题(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.
13.我国“南仓”级远洋综合补给舰满载排水量为37000吨,把数37000用科学记数法表示为 。
14.计算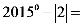 。
。
15. 已知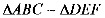 ,
,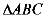 与
与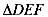 的相似比为4:1,
的相似比为4:1,
则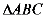 与
与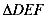 对应边的高之比为 。
对应边的高之比为 。
16. 如图,在等腰直角三角形ABC中,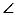 ACB=90°,AB=
ACB=90°,AB=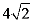 ,以A为
,以A为
圆心,AC长为半径作弧,交AB于点D,则阴影部分 的面积是 。
的面积是 。
17. 从
从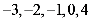 这五个数中随机抽取一个数记为
这五个数中随机抽取一个数记为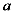 ,
,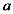 的值既是不等式组
的值既是不等式组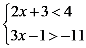 的解,又在函数
的解,又在函数 的自变量取值范围内的概率是 。
的自变量取值范围内的概率是 。
18.如图,矩形ABCD中,AB=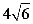 ,AD=10,连接BD,
,AD=10,连接BD,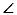 DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△
DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△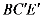 ,当射线
,当射线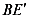 和射线
和射线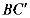 都与线段AD相交时,设交点分别F,G,若△BFD为等腰三角形,则线段DG长为
都与线段AD相交时,设交点分别F,G,若△BFD为等腰三角形,则线段DG长为  。
。
三、解答题:(本大题2个小题,每小题7分,共14分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
19.解方程组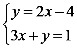
20. 如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,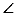 B=
B=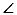 E。
E。
求证: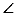 ADB=
ADB=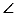 FCE.
FCE.
四、解答题:(本大题4个小题,每小题10分,共40分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
21.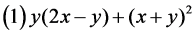

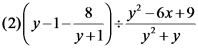
22. 为贯彻政府报告中“全民创新,万众创业”的精神,某镇对辖区内所有的小微企业按年利润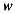 (万元)的多少分为以下四个类型:A类(
(万元)的多少分为以下四个类型:A类(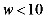 ),B类(
),B类(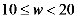 ),C类(
),C类(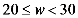 ),D类(
),D类(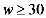 ),该镇政府对辖区对辖区内所有的小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
),该镇政府对辖区对辖区内所有的小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
(1)该镇本次统计的小微企业总个数是 。扇形统计图中B类所对应扇形圆心角的度数为 度。请补全条形统计图。
(2)为进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会,计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中2个来自高新区,另2个来自开发区,请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率。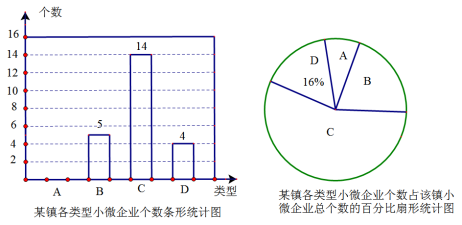
23.如果把一个自然数各数位上数字从最高位到个位依次排出一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数叫做“和谐数”.例如:自然数64746从最高位到个位排出的一串数字是:6、4、7、4、6,从个位 到最高排出的一串数字也是:6、4、7、4、6,所64746是“和谐数”.再如:33,181,212,4664,…,都是“和谐数”.
到最高排出的一串数字也是:6、4、7、4、6,所64746是“和谐数”.再如:33,181,212,4664,…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”,猜想任意一个四位“和谐数”能否被11整除,并说明理由;
(2) 已知一个能被11整除的三位“和谐数”,设个位上的数字为x(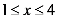 ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式.
24. 某水库大坝的横截面是如图所示的四边形BACD,期中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角 ,观测渔船N在俯角
,观测渔船N在俯角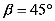 ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度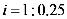 .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为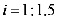 ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据: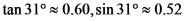 )
)
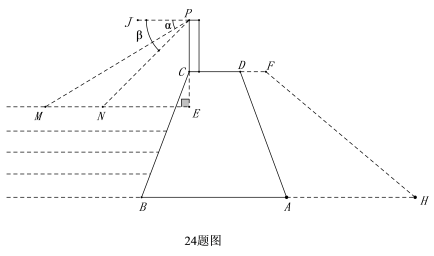
五、解答题:(本大题2个小题,每小题12分,共24分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上 .
.
25.如图1,在△ABC中,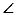 ACB=90°,
ACB=90°,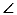 BAC=60°,点E角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF。
BAC=60°,点E角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF。
(1)如图1,若点H是AC的中点,AC=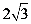 ,求AB
,求AB ,BD的长。
,BD的长。
(2)如图1,求证:HF=EF。
(3)如图2,连接CF,CE,猜想:△CEF是否是等边三角形?若是,请证明;若不是,请说明理由。
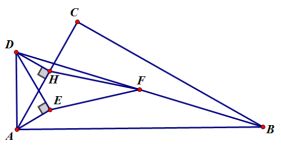
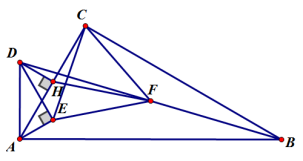
图1 图2
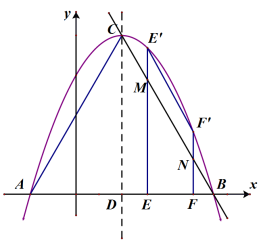
26. 如图1,在平面直角坐标系中,抛物线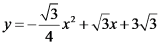 交
交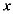 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交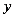 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与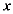 轴的交点为D。
轴的交点为D。
(1)求直线BC的解析式。
(2)点E(m,0),F(m+2,0)为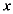 轴上两点,其中
轴上两点,其中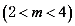 ,
,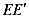 ,F
,F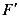 分别垂直于
分别垂直于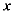 轴,交抛物线与点
轴,交抛物线与点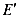 ,
,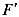 ,交BC于点M,N,当
,交BC于点M,N,当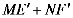 的值最大时,在
的值最大时,在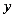 轴上找一点R,使得
轴上找一点R,使得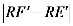 值最大,请求出R点的坐标及
值最大,请求出R点的坐标及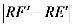 的最大值。
的最大值。
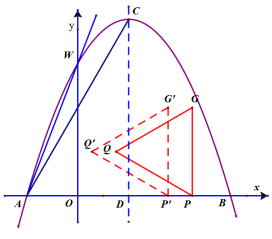
(3)如图2,已知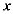 轴上一点
轴上一点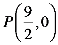 ,现以点P为顶点,
,现以点P为顶点,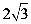 为边长在
为边长在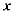 轴上方作等边三角形QPC,使GP⊥
轴上方作等边三角形QPC,使GP⊥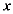 轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为
轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为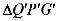 ,设
,设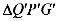 与△ADC的重叠部分面积为s,当点
与△ADC的重叠部分面积为s,当点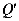 到
到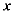 轴的距离与点到直线AW的距离相等时,求s的值。
轴的距离与点到直线AW的距离相等时,求s的值。
图2 |
图1 |
数学试题(A卷)参考答案
(全卷共五个大题 满分150分 考试时间120分钟)
一、选择题(本大题12个小题,每小题4分,共48分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | A | B | A | B | C | C | D | B | C | B | D |
二、填空题(本大题共6个小题,每小题4分,共24分)
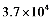
13. -1
14. 4:1
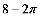
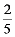
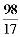
三、解答题(本大题共2个小题,每小题7分,共14分)
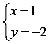
∵BC=DE
∴BC+CD=DE+CD
即BD=CE
易证:△ABD≌△FEC
故: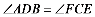
四、解答题(本大题4个小题,每小题10分,共40分)
15.
⑴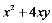
⑵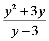
16.
⑴25;72;图略
⑵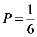
17.
⑴四位“和谐数”:1111, 2222,3443,1221等
2222,3443,1221等
任意一个四位“和谐数”都能被11整数,理由如下:
设四位“和谐数”是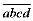 ,则满足:
,则满足:
个位到最高位排列: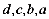
最高位到个位排列: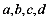
由题意,两组数据相同,则: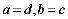
则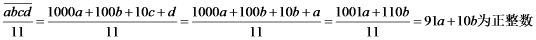 所以四位“和谐数”
所以四位“和谐数”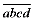 能被11整数
能被11整数
又由于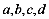 的任意性,故任意四位“和谐数”都可以被11整除
的任意性,故任意四位“和谐数”都可以被11整除
⑵设能被11整除的三位“和谐数”为: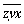 ,则满足:
,则满足:
个位到最高位排列:
最高位到个位排列: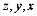
由题意,两组数据 相同,则:
相同,则: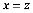
故
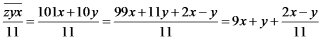 为正整数
为正整数
故
18.
⑴在Rt△PEN中,EN=PE=30m
在Rt△PEM中,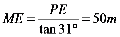
∴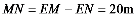
答:两渔船M、N之间的距离为20米
⑵过点D作DN⊥AH交直线AH于点N
由题意: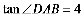 ,
,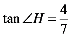
在RT△DAN中,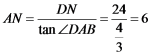 m
m
在RT△DHN中,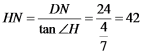 m
m
故AH=HN-AN=42-6=36m
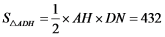

故需要填筑的土石方共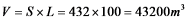
设原计划平均每天填筑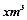 ,则原计划
,则原计划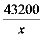 天完成;增加机械设备后,现在平均每天填筑
天完成;增加机械设备后,现在平均每天填筑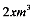
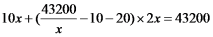
解得: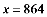
经检验: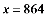 是原分式方
是原分式方 程的解,且满足实际意义
程的解,且满足实际意义
答:该施工队原计划平均每天填筑864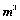 的土石方
的土石方
五、解答题(本大题共2个小题,每小题12分,共24分)
19.
⑴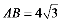 ,
,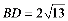
⑵连接AF
易证:△DAE≌△ADH,故DH=AE
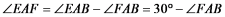
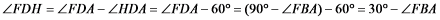
故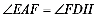
易证:△DHF≌△AEF
∴H F=EF
F=EF
⑶(方法不唯一,有很多,合理即可)
(法一)取AB的中点M,连接CM、FM
在RT△ADE中,AD=2AE
FM是△ABD的中位线,故AD=2FM
∴FM=AE
易证△ACM为等边三角形,故AC=CM
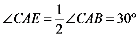
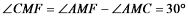
故△ACE≌△MCF(手拉手全等模型)
故易证:△CEF为等边三角形

(法二)延长DE至点N,使EN=DE,连接AN;延长BC至点M,使CB=CM,连接AM;延长BD交AM于点P
易证:△ADE≌△ANE,△ABC≌△AMC
易证:△ADM≌△ANB(手拉手全等模型),故DM=BN
CF是△BDM的中位线,EF是△BDN的中位线
故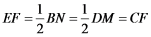

故△CEF为等边三角形

⑴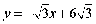
⑵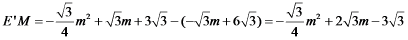

故: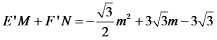
当 时,
时,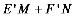 最大,
最大,
此时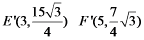
∴
∴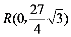 ,
,
⑶由题意,Q点在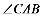 的角平分线或外
的角平分线或外 角平分线上
角平分线上
①当Q点在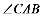 的角平分线上时,如图
的角平分线上时,如图
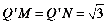 ,
,
△RMQ’∽△RNC,故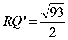 ,则
,则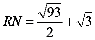
△CRN∽△CWO,故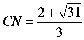
∴DN=CD-CN=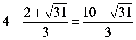
故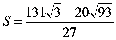

②当Q点在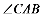 的外角平分线上时,如图
的外角平分线上时,如图
△Q’RN∽△WCO,故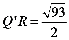 ,故
,故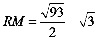
△RCM∽△WCO,故CM=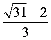
在Rt△Q’MP’中,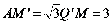 ,故
,故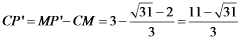
在Rt△CP’S中,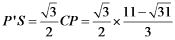
故S=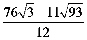
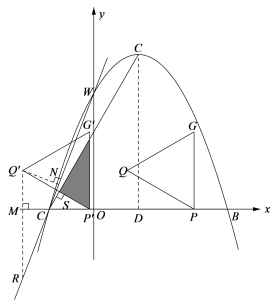
















![等级考试] 软考网络工程师闯关密卷讲解视频 2013-2015年 真题试卷答案及解析](https://static.kouhao8.com/sucaidashi/xkbb/df19200c0018d6b0be6f61852e7fe580.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)



![2022全国新高考I卷、乙卷、北京卷数学、语文真题附答案解析[百度网盘分享]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/25-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)







相关资源