2021年全国高中数学联赛几何题思路分析

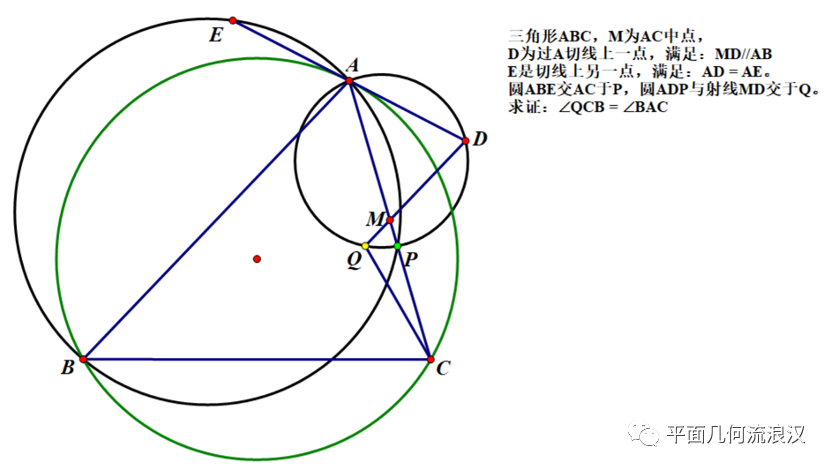
（一）

这道题的一些点的生成方式还是比较奇怪的，但它们又都是被三角形ABC定下的，这就需要我们先熟悉一下它们。

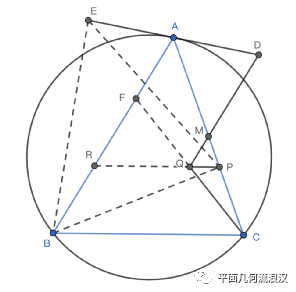
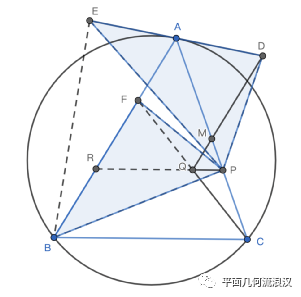
笔者首先重画了图，因为我觉得圆AEBM，圆ADQ使图变得太复杂，而复杂会影响我们对性质的探索，笔者一般用交叉状的四点共圆来利用圆，于是重画图如下：

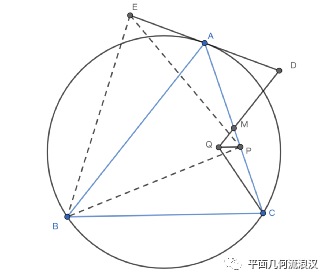
圆很多，还有切线，那肯定有很多导角的空间，不妨试试：

,而AB//DQ，故必有PQ//BC（这个也能直接看图观察出来）(并且这样的话如果延长DQ和AC相交，由能再得一个四点共圆,不过好像没什么用)

又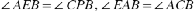,马上有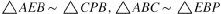(由旋转相似前者能推出后者)，进而（直接看这有很多等角，但不知道怎么用），考虑到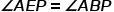,那么如果延长PQ和AB相交就能产生一组相似：

即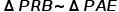，如图，当然可以再来次旋转相似，但都是些较显然的结论。

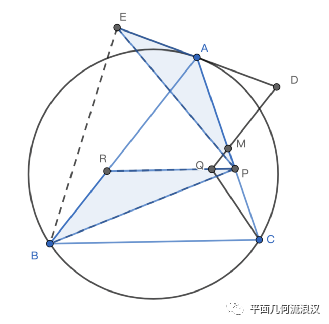
图*

到这里又不知道该怎么办了，其实如果观察得仔细些还会发现QM是三角形ABC中位线，所以DM是过BC中点的。对这个图有了一次最初的探索后，再得看看结论了。如果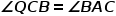,那么，如果延长CQ与AB相交：

那么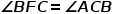，即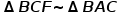（还是没什么用），另一方面，那么一定有AFQP四点共圆，结合ADPQ四点共圆，即一定是ADPQF五点共圆，反过来，如果我证出这个五点共圆，则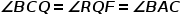，这题就做出来了路。这就有些东西了，因为AFQD四点共圆，又有AF//QD，那么AFQD一定是等腰梯形，即必有FQ=AD，马上EA=DA=CQ=FQ，然后我就想着如何证边等……然后放弃（我陷入了一个又一个循环。。。）还是要换方向……图*的那个旋转相似再一次吸引了我，因为两个三角形都有一条边被倍长了，并且它们还是对应边！马上，连PF，PD，哦！做出来了！

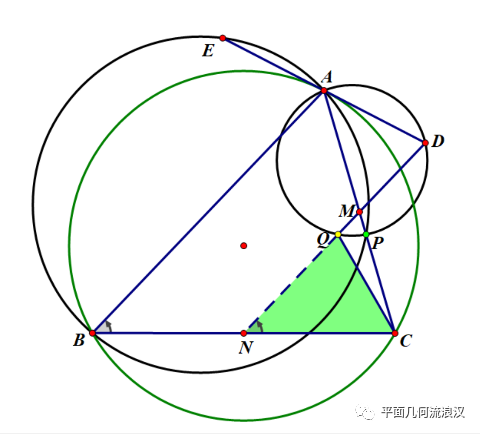
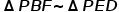由便推出，进而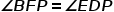，AFDP四点共圆，于是ADPQF五点共圆，结束！

回头来看的话，前面那些误打误撞遇到的结论也就都成立了。

另一种方法与答案类似，那是如何想到的呢？

（二）

除了三角形ABC，就再也没有可以自由活动的点了。点的生成顺序是红点->绿点->黄点。点的生成顺序在每个问题的分析里都很重要，我之前反复强调过。

可见P，Q属于困难点。暂时没有现成性质可以用。那么再看看要证明的结论：角相等。两个角度的位置不好，那就做转化：直接倒角，亦或把对应的角放入一组相似，或者找四点共圆。

这里经过简单的尝试，我们把这两个角放入了一组相似三角形里：三角形QCN（N为BC中点）和三角形CAB。见下图。因为有一组角相等是很显然的，所以只需证相等角的两边对应的比例关系了。即：

图二，只需证一组相似

好了，观这两组边，居然有三个都和三角形ABC有直接关系（CB，AB，NC）！这就开心了啊！那就和一试的思路一样，只需把不知道的QN用三角形ABC是三边表示即可！

QN往哪里去转化呢，一个很自然的思路就是把QN放入我们熟悉的边关系里去，比如圆幂，勾股，等腰，相似等等。这个时候利用简单的尝试和观察，注意到QP//NC（简单利用平行和弦切角倒角），我们有：

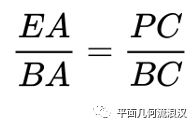
乘胜追击！发现MN，CM又是已知量，所以只需要求出PC长度！最困难的Q被我们消掉了！！

图三，问题转化（1）

那么PC又怎么求呢？实际上就是把转化QN的方法再使用了一次。

先画出把Q消除的简化版新图：

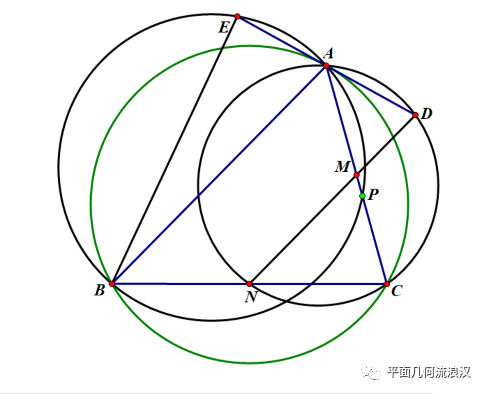
图四，消点Q

观察几何元素。这个时候我们敏锐的察觉图中的相等角度很多，果不其然，有一组相似，正是我们想要的！见下图（涂色的两个三角形相似，自己证，此处从略！）

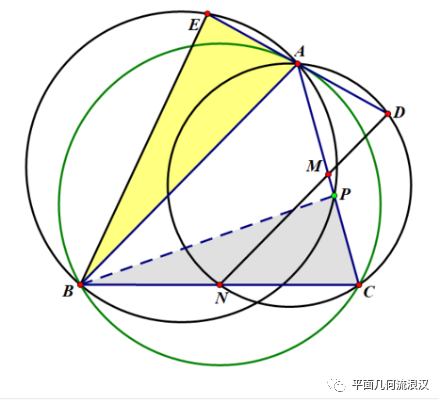
图五，问题转化（2）

所以，

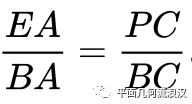
这时只需要求出AE（= AD）的长度！次困难的P也被我们消掉了。甚至可以消掉E,那么图就成了这样：

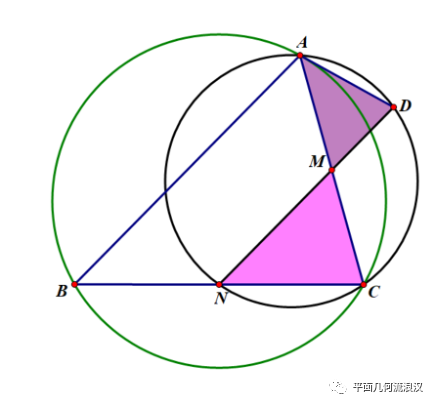
图五，问题转化（3）

这个时候用肉眼可见的一组相似，得到：

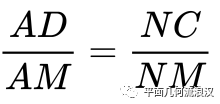
这个式子除了AD其他均已知，故问题得证。

写解答时就把我的分析反过来，最后一步“装作”自己无意“发现”了三角形QCN和三角形CAB相似（其实这是分析的切入口）。做完。

这个题考的就是分析能力。

做完这个题，我们能得到什么启示呢？