高中数学求函数值域问题的六种方法
发布于 2021-08-12 19:50 ,所属分类:高考数学学习资料大全
一、反函数法
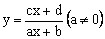 的值域,这种类型的题目也可采用分离常数法。
的值域,这种类型的题目也可采用分离常数法。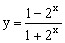 的值域。
的值域。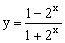 解得
解得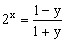
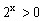 ,所以
,所以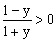 ,则
,则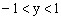
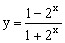 的值域为
的值域为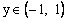 。
。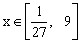 ,求函数
,求函数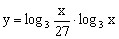 的值域。
的值域。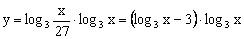
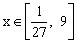 ,则
,则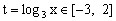

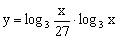 的值域是
的值域是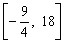 。
。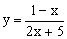 的值域。
的值域。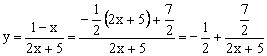
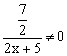 ,则
,则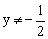
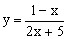 的值域为
的值域为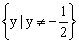 。
。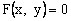 ,通过方程有实数根,根据判别式
,通过方程有实数根,根据判别式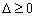 ,从而求得原函数的值域
,从而求得原函数的值域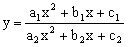 (
(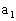 、
、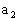 不同时为0)的值域,常用此方法求解。
不同时为0)的值域,常用此方法求解。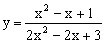 的值域。
的值域。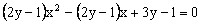 。
。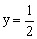 时,方程无解;
时,方程无解;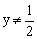 时,因为
时,因为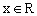
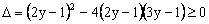
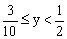 。
。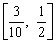 。
。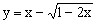 的值域。
的值域。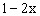 随
随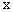 的增大而减少,
的增大而减少,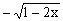 随
随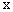 的增大而增大,所以函数
的增大而增大,所以函数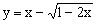 在定义域
在定义域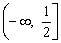 上是增函数。
上是增函数。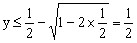 ,所以函数
,所以函数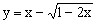 的值域为
的值域为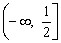 。
。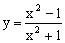 的值域。
的值域。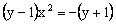
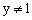 ,所以
,所以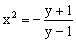
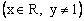
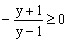 ,故
,故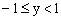 所以函数
所以函数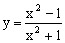 的值域为
的值域为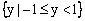 。
。

























相关资源