高中数学导数知识总结+导数七大题型答题技巧!
发布于 2021-09-11 13:47 ,所属分类:数学资料学习库

最新高考资讯,志愿填报指导,志愿智能设计,职业兴趣测评,历年录取查询,就找梦中的航标,给你指导方向,让你圆理想的大学
还在为孩子的成绩一直平平无奇感到焦虑吗?
还在为孩子由于作业压力而痛苦吗?
还在担心孩子到学习负担而耽误成长吗?
专家来支招啦!!!
梦中到航标特聘专家:
多年从事孩子到心理辅导
专业解决孩子与父母发青春期矛盾
为孩子制定符合自身的学习方法
你们的高考之路,我们一路相伴
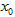 处的瞬时变化率是
处的瞬时变化率是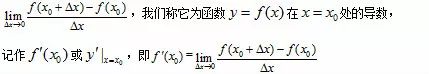
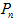 趋近于P时,直线 PT 与曲线相切。容易知道,割线的斜率是
趋近于P时,直线 PT 与曲线相切。容易知道,割线的斜率是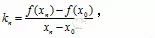
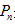 趋近于 P 时,函数y=f(x)在x=
趋近于 P 时,函数y=f(x)在x=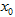 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即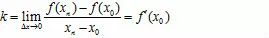
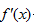 便是x的一个函数,我们称它为f(x)的导函数. y=f(x)的导函数有时也记作
便是x的一个函数,我们称它为f(x)的导函数. y=f(x)的导函数有时也记作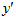 ,即
,即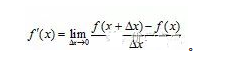
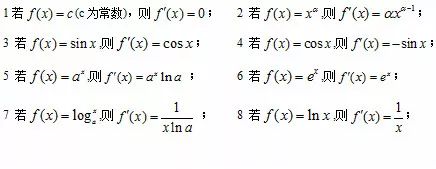
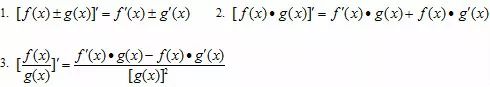
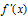 >0,那么函数y=f(x)在这个区间单调递增;
>0,那么函数y=f(x)在这个区间单调递增;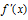 <0,那么函数y=f(x)在这个区间单调递减;
<0,那么函数y=f(x)在这个区间单调递减;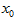 附近的左侧
附近的左侧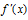 >0 ,右侧
>0 ,右侧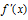 <0,那么
<0,那么 是极大值;
是极大值;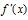 <0 ,右侧
<0 ,右侧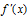 >0,那么
>0,那么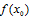 是极小值;
是极小值;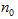 )时成立,这是递推的基础;
)时成立,这是递推的基础;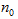 ,且n∈N)结论都成立。
,且n∈N)结论都成立。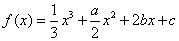 ,当
,当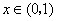 时取得极大值,当
时取得极大值,当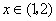 时取得极小值,求点
时取得极小值,求点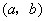 对应的区域的面积以及
对应的区域的面积以及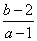 的取值范围.
的取值范围.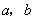 的线性不等关系,点
的线性不等关系,点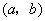 所对应的区域.第(2)问利用斜率求出
所对应的区域.第(2)问利用斜率求出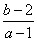 的取值范围.
的取值范围.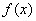 的导数为
的导数为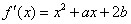 ,当
,当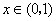 时取得极大值,当
时取得极大值,当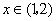 时取得极小值,则方程
时取得极小值,则方程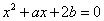 有两个根,一个根在区间
有两个根,一个根在区间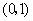 内,另一个根在区间(1,2)内.
内,另一个根在区间(1,2)内.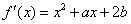 的图象与方程
的图象与方程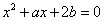 的根的分布之间的关系可以得到
的根的分布之间的关系可以得到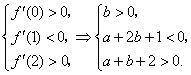
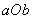 平面内满足约束条件的点
平面内满足约束条件的点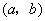 所对应的区域为
所对应的区域为 (不包括边界,其中点
(不包括边界,其中点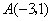 ,
,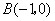 ,
,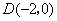 如右图所示).
如右图所示).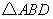 的面积为
的面积为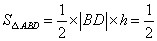 (
(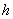 为点
为点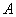 到
到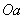 轴的距离)
轴的距离) 与点
与点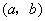 连线的斜率为
连线的斜率为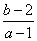 ,显然
,显然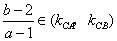 ,即
,即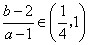 .
.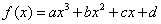 是定义在
是定义在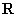 上的函数,其图象交
上的函数,其图象交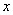 轴于
轴于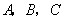 三点.若点
三点.若点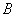 的坐标为
的坐标为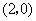 ,且
,且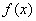 在
在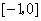 和
和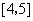 上有相同的单调性,在
上有相同的单调性,在 和
和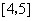 上有相反的单调性.
上有相反的单调性. 的值;
的值;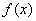 的图象上是否存在一点
的图象上是否存在一点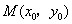 ,使得
,使得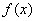 在点
在点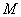 的切线斜率为
的切线斜率为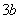 ?
?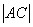 的取值范围.
的取值范围.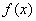 在
在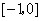 和
和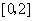 上有相反的单调性,
上有相反的单调性,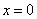 是
是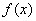 的一个极值点.
的一个极值点.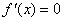 ,即
,即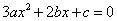 有一个解为
有一个解为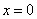 ,
,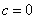 .
.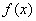 交
交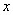 轴于点
轴于点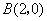 ,所以
,所以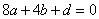 ,即
,即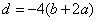 .
.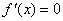 ,得
,得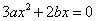 ,
,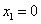 ,
, .
.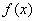 在
在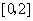 和
和 上有相反的单调性,
上有相反的单调性,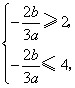 ,
, .
.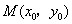 ,使得
,使得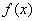 在点
在点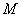 的切线斜率为
的切线斜率为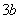 .
.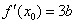 ,
,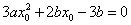 .
.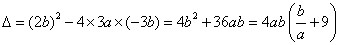 .
.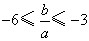 ,
,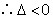 .
.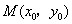 ,使得
,使得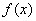 在点
在点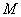 的切线斜率为
的切线斜率为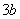 .
.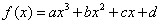 的函数图象交
的函数图象交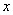 轴于点
轴于点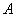 的坐标为
的坐标为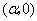 、点
、点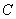 的坐标为
的坐标为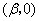 .
.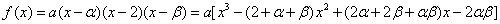 ,
,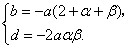 .得
.得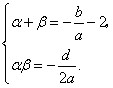 .
.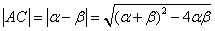 ,
,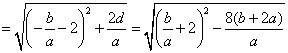 ,
,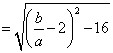 ,
,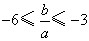 ,∴当
,∴当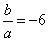 时,
时,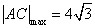 ;当
;当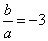 时,
时,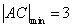 .故
.故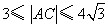 .
.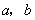 的值,大大简化了运算.运用整体思想解题是不是很巧妙?这种整体思想在其它知识板块中都有广泛的应用,在以后的学习中可要留心哟.
的值,大大简化了运算.运用整体思想解题是不是很巧妙?这种整体思想在其它知识板块中都有广泛的应用,在以后的学习中可要留心哟.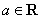 ,求
,求 的单调区间.
的单调区间.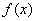 的导数
的导数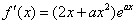 .
.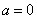 时,若
时,若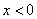 ,则
,则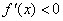 ;若
;若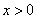 ,则
,则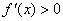 .
.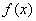 在
在 内为减函数,在
内为减函数,在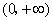 内为增函数.
内为增函数.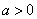 时,由
时,由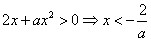 或
或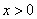 ,
,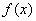 在
在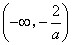 或
或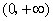 内为增函数,在
内为增函数,在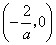 内为减函数.
内为减函数.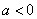 时,由
时,由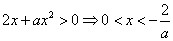 ,
,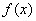 在
在 内为增函数,在
内为增函数,在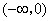 和
和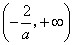 内为减函数.
内为减函数.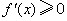 函数为增函数,
函数为增函数,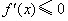 函数为减函数.但要确定
函数为减函数.但要确定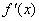 的符号,须对参数进行分类讨论.
的符号,须对参数进行分类讨论. ,
,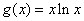 .
.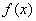 的最大值.
的最大值.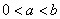 ,证明:
,证明: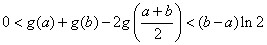 .
.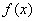 的定义域是
的定义域是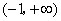 ,则
,则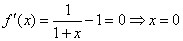 .
.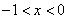 时,
时,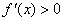 ;
;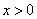 时,
时,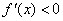 .
.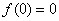 ,则当且仅当
,则当且仅当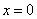 时,
时, 取最大值0.
取最大值0.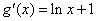 ,设
,设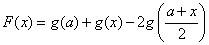 .
.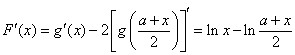 .
.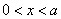 时,
时, ,
,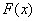 在
在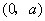 内为减函数;
内为减函数;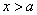 时,
时,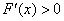 ,
,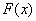 在
在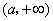 内为增函数.
内为增函数.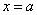 时,
时,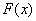 有极小值
有极小值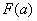 .
.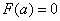 ,
,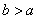 ,
,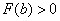 ,即
,即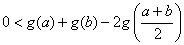 .
.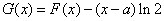 ,
,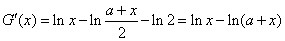 ,
,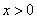 时,
时,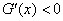 ,
,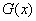 在
在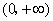 上为减函数.
上为减函数.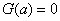 ,
,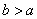 ,所以
,所以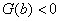 ,
,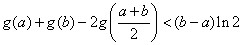 .
.








































相关资源